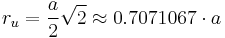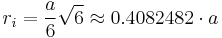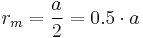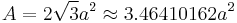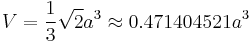Octahedron
| Regular Octahedron | |
|---|---|
(Click here for rotating model) |
|
| Type | Platonic solid |
| Elements | F = 8, E = 12 V = 6 (χ = 2) |
| Faces by sides | 8{3} |
| Schläfli symbol | {3,4} |
| Wythoff symbol | 4 | 2 3 |
| Coxeter-Dynkin | |
| Symmetry | Oh, [4,3], (*432) |
| References | U05, C17, W2 |
| Properties | Regular convex deltahedron |
| Dihedral angle | 109.47122° = arccos(-1/3) |
3.3.3.3 (Vertex figure) |
Cube (dual polyhedron) |
Net |
|
In geometry, an octahedron (plural: octahedra) is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
An octahedron is the three-dimensional case of the more general concept of a cross polytope.
Contents |
Dimensions
If the edge length of a regular octahedron is  , the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is
, the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is
and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is
while the midradius, which touches the middle of each edge, is
Cartesian coordinates
An octahedron can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates of the vertices are then
- ( ±1, 0, 0 );
- ( 0, ±1, 0 );
- ( 0, 0, ±1 ).
Area and volume
The surface area A and the volume V of a regular octahedron of edge length a are:
Thus the volume is four times that of a regular tetrahedron with the same edge length, while the surface area is twice (because we have 8 vs. 4 triangles).
Geometric relations
The interior of the compound of two dual tetrahedra is an octahedron, and this compound, called the stella octangula, is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids. One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound.
Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space, called the octet truss by Buckminster Fuller. This is the only such tiling save the regular tessellation of cubes, and is one of the 28 convex uniform honeycombs. Another is a tessellation of octahedra and cuboctahedra.
The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess mirror planes that do not pass through any of the faces.
Using the standard nomenclature for Johnson solids, an octahedron would be called a square bipyramid. Truncation of two opposite vertices results in a square bifrustum.
The octahedron is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.[1]
Uniform colorings and symmetry
There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.
The octahedron's symmetry group is Oh, of order 48, the three dimensional hyperoctahedral group. This group's subgroups include D3d (order 12), the symmetry group of a triangular antiprism; D4h (order 16), the symmetry group of a square bipyramid; and Td (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.
| Name | Octahedron | Rectified tetrahedron (Tetratetrahedron) | Triangular antiprism | Square bipyramid |
|---|---|---|---|---|
| Coxeter-Dynkin | ||||
| Schläfli symbol | {3,4} | t1{3,3} | s{3,2} | |
| Wythoff symbol | 4 | 3 2 | 2 | 4 3 | 2 | 6 2 | |
| Symmetry | Oh [4,3] (*432) |
Td [3,3] (*332) |
D3d [2+,6] (2*3) |
D4h [2,3] (*322) |
| Symmetry order | 48 | 24 | 12 | 16 |
| Image (uniform coloring) |
(1111) |
(1212) |
(1112) |
Dual
The octahedron is the dual polyhedron to the cube.
Nets
It has eleven arrangements of nets.
This example depicts it as both a dipyramid and an antiprism:
Related polyhedra
Tetratetrahedron
The regular octahedron can also be considered a rectified tetrahedron - and can be called a tetratetrahedron. This can be shown by a 2-color face model. With this coloring, the octahedron has tetrahedral symmetry.
Compare this truncation sequence between a tetrahedron and its dual:
Tetrahedron |
Truncated tetrahedron |
Octahedron |
Truncated tetrahedron |
Tetrahedron |
The above shapes may also be realized as slices orthogonal to the long diagonal of a tesseract. If this diagonal is oriented vertically with a height of 1, then the five slices above occur at heights  , 3/8, 1/2, 5/8, and
, 3/8, 1/2, 5/8, and  , where
, where  is any number in the range (0,1/4], and
is any number in the range (0,1/4], and  is any number in the range [3/4,1).
is any number in the range [3/4,1).
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,9} |
| Name | tetrahedron | rectified tetrahedron (octahedron) |
truncated tetrahedron | cantellated tetrahedron (cuboctahedron) |
omnitruncated tetrahedron (truncated octahedron) |
Snub tetrahedron (icosahedron) |
|---|---|---|---|---|---|---|
| Schläfli | {3,3} | t1{3,3} | t0,1{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| Coxeter-Dynkin | ||||||
| Graph (A3) |
||||||
| Graph (A2) |
||||||
| Solid | ||||||
| Tiling |
Tetrahemihexahedron
The regular octahedron shares its edges and vertex arrangement with one nonconvex uniform polyhedron: the tetrahemihexahedron, with which it shares four of the triangular faces.
Octahedron |
Tetrahemihexahedron |
Octahedra in the physical world
- Especially in roleplaying games, this solid is known as a "d8", one of the more common non-cubical dice.
- If each edge of an octahedron is replaced by a one ohm resistor, the resistance between opposite vertices is 1/2 ohms, and that between adjacent vertices 5/12 ohms.[2]
- Natural crystals of diamond, alum or fluorite are commonly octahedral, as the space=filling tetrahedral-octahedral honeycomb.
- The plates of kamacite alloy in octahedrite meteorites are arranged paralleling the eight faces of an octahedron.
- Many metal ions coordinate six ligands in an octahedral or distorted octahedral configuration.
Octahedra in music
Six musical notes can be arranged on the vertices of an octahedron in such a way that each edge represents a consonant dyad and each face represents a consonant triad; see hexany.
Other octahedra
The following polyhedra are combinatorially equivalent to the regular polyhedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of a regular octahedron.
- Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles.
- Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilaterals are planar squares.
- Schönhardt polyhedron, a nonconvex polyhedron that cannot be partitioned into tetrahedra without introducing new vertices.
More generally, an octahedron can be any polyhedron with eight faces. The regular octahedron has 6 vertices and 12 edges, the minimum for an octahedron; nonregular octahedra may have as many as 12 vertices and 18 edges.[1] Other nonregular octahedra include the following.
- Hexagonal prism: Two faces are parallel regular hexagons; six squares link corresponding pairs of hexagon edges.
- Heptagonal pyramid: One face is a heptagon (usually regular), and the remaining seven faces are triangles (usually isosceles). It is not possible for all triangular faces to be equilateral.
- Truncated tetrahedron. The four faces from the tetrahedron are truncated to become regular hexagons, and there are four more equilateral triangle faces where each tetrahedron vertex was truncated.
- Tetragonal trapezohedron. The eight faces are congruent kites.
See also
- Spinning octahedron
- Stella octangula
- Triakis octahedron
- Hexakis octahedron
- Truncated octahedron
- Octahedral molecular geometry
- Octahedral symmetry
- Octahedral graph
References
- ^ Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010). "On well-covered triangulations. III". Discrete Applied Mathematics 158 (8): 894–912. doi:10.1016/j.dam.2009.08.002. MR2602814.
- ^ Klein, Douglas J. (2002). "Resistance-Distance Sum Rules" (PDF). Croatica Chemica Acta 75 (2): 633–649. http://jagor.srce.hr/ccacaa/CCA-PDF/cca2002/v75-n2/CCA_75_2002_633_649_KLEIN.pdf. Retrieved 2006-09-30.
External links
- Weisstein, Eric W., "Octahedron" from MathWorld.
- Richard Klitzing, 3D convex uniform polyhedra, x3o4o - oct
- Editable printable net of an octahedron with interactive 3D view
- Paper model of the octahedron
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
|
|
|||||
|
||||||||||||||||||||||||||